Tackle Word Problems in STRIDE

834

“Math is my worst subject,” I often thought growing up. Never was this fact more evident than when my teacher presented me with a word problem. My mother, a veteran middle school math teacher, worked math problems and read Algebra textbooks the way I do books on writing. But the calculus of word problems continued to escape me even into college.

It’s no surprise that word problems intimidate. Having a framework to build problem-solving mastery may make the difference for students like me. I often wished for a simple approach to solving math problems, but my mother, who taught math for many years successfully, never gave me one approach or model. I always wonder, if we offered students one model or approach to use consistently, would that would work? Perhaps like George Polya’s approach or the STRIDE Model, which I will focus on in this blog.

Update: Lynn has made a compelling argument for modifying the STRIDE Model in the comments. I’ve responded with a revised model that seeks to capture the critique in her remarks. I’ve also included the revised version with a new infographic at the end of this blog post. You decide which is the better model, version 1 or version 2. My thanks to my readers for assisting me in learning how to solve math word problems, to leverage comprehension while solving them.

The STRIDE Model v1

The STRIDE Model (Scan, Think, Reflect, Identify, Do, Evaluate) equips learners with systematic steps. It facilitates breaking down problems into steps. The Model aligns itself to schema-based instruction, and critical thinking. Let’s explore how to integrate STRIDE into classrooms with grade-specific activities, templates, and actionable infographics.

Let me know what you think, non-math experts and fellow bewildered word problem-solvers. Does STRIDE work for you?

An Example Solution: The STRIDE Framework

Let’s explore what this might look like below. If you’re a math teacher, I hope you’ll double-check the math and share your thoughts in the comments. Be kind, I’m not a math person and I totally relied on AI for support.

1. Scan the Problem

• Numbers:
  • Truck speed = 60 mph,
  • Car speed = 66 mph,
  • Head start = 13 minutes.
• Key Words: “13 minutes later,” “pass the truck.”

2. Think About Connections

• Relate to real-life highway overtaking.
• Visualize the truck’s head start as a distance gap.

3. Reflect on the Question

• Rephrase: “How long will the car take to close the 13-minute distance gap created by the truck?”

4. Identify a Strategy

Calculate the truck’s head start distance:

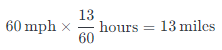
Determine the car’s relative speed:

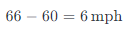
5. Do the Work

Time to catch up:

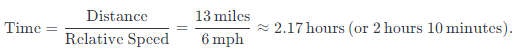
6. Evaluate Your Answer
Verify both of these items:
a) Truck’s distance after 2.17 hours:

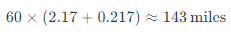
b) Car’s distance:

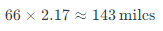
Digital Templates

Below, you will find a chart that clarifies each stage of the STRIDE strategy, along with some sample ideas for activities. You can find a Canva template link to the STRIDE Model here.

Strategy	Activities	Focus
Scan the Problem	Problem dissection worksheets; keyword highlighting in multi-step problems	Circle numbers, underline keywords
Think About Connections	Drawing diagrams; writing real-life scenarios to contextualize problems	Real-life connections, diagrams
Reflect on the Question	Rephrasing exercises (individual worksheets and group comparisons)	Goal identification, self-check prompts
Identify a Strategy	Strategy justification; challenge prediction during planning	Brainstorming, step-by-step planning
Do the Work	Step-by-step demonstrations (interactive whiteboards); collaborative solving	Showing work, explaining logic

Give it a go! Try students out on the STRIDE Model, a schema-based framework for solving word problems. You never know, it may assist them as they work to solve problems.

STRIDE Model v2

As promised, here’s the revised model. What do you think? How could it be improved based on your knowledge and experiences?

S – Survey the Situation:

• Read the entire problem carefully to understand the overall story or context. What is happening in the problem?
• Identify all the important information given: What facts or details do you know? (Make sure to include numbers and their units or labels).
• Briefly consider what the problem might be asking you to find or do (you’ll refine this in step R).

T – Think About Connections:

• Connect the problem to what you already know (similar problems, real-world experiences).
• Visualize or draw the situation described in the problem to help build understanding and see relationships between the pieces of information.

R – Reflect on the Question:

• Ask yourself: What specifically is the problem asking me to find or do? What will the answer look like (e.g., a number of apples, a measurement, a comparison)?
• Rephrase the question in your own words to ensure you understand the goal.

I – Identify a Strategy:

• Based on your understanding of the situation and the question, decide what mathematical steps, operations, or procedures will help solve the problem (e.g., addition, subtraction, multiplication, division, drawing a diagram, making a table).
• Consider if there are multiple steps needed. Use tools like graphic organizers or charts if they help plan your approach.

D – Do the Work:

• Carry out your chosen strategy step by step.
• Show your work clearly and write down your reasoning to track your thinking process and make it easier to review. Check calculations as you go.

E – Evaluate Your Answer:

• Check your final answer: Does it make sense in the context of the situation you surveyed in step S? Is the unit appropriate for the question asked in step R?
• Review your steps (D). If the answer seems unreasonable, revisit your understanding (S, T, R) or your strategy (I) and try again.

Revised Infographic for the STRIDE Model v2

Here’s a quick revision featuring the STRIDE Model v2. Be sure to review each step with a critical eye, and remember that I am challenged in both art and math. 🙂